Chapter 7.1-7.2 Notes

Steps for solving ANY 2-d force problem:

A. Draw a free body diagram.

B. List all forces in the x direction

C. List all forces in the y direction

D. List all forces that are not in the x or y direction

E. Draw a triangle for each force in step D with the x and y components.

F. Break down all of the forces from step D into their x and y direction components.

G. Write the net force equation for the x direction (the sum of all the x direction forces).

H. Write the net force equation for the y . direction (the sum of all the y direction forces).

I. Determine the acceleration in the x direction.

J. Determine the acceleration in the y direction.

K. Determine the net force using F net=ma for the x direction.

L. Determine the net force using F net=ma for the y direction.

Click here for help on determining the coefficient of friction for a block sliding down the ramp at a constant velocity.

7.1: Equilibrium and the Equilibrant

An object is in equilibrium when the net force on it is zero. Net force may be the resultant of 2 or more forces acting concurrently, but the sum of all these forces is zero.

Such a condition means that the object is either at rest or in motion with a constant velocity (acceleration = zero) .

If the sum of all the forces acting concurrently is not qero, then the object is not in equilibrium

If one more force can be added that will bring the object into equilibrium, such a force is called the equilibrant.The equilibrant is equal in magnitude to the non-zero resultant of all other forces, but opposite in direction.

Gravitational Force and Inclined Planes
These represent an important class of problems involving sliding boxes up and down an inclined plane where you have friction. In the following instance, imagine a block of wood set on a wooden ramp. The ramp is slowly raised from horizontal while someone taps the ramp with a finger to cause a vibration, which prevents static friction. The ramp is raised to the point where the block just begins to slide. At this point, the frictional force, Ff which points up the ramp has just been equaled by the applied force, supplied by the component of gravity pointing down the ramp!

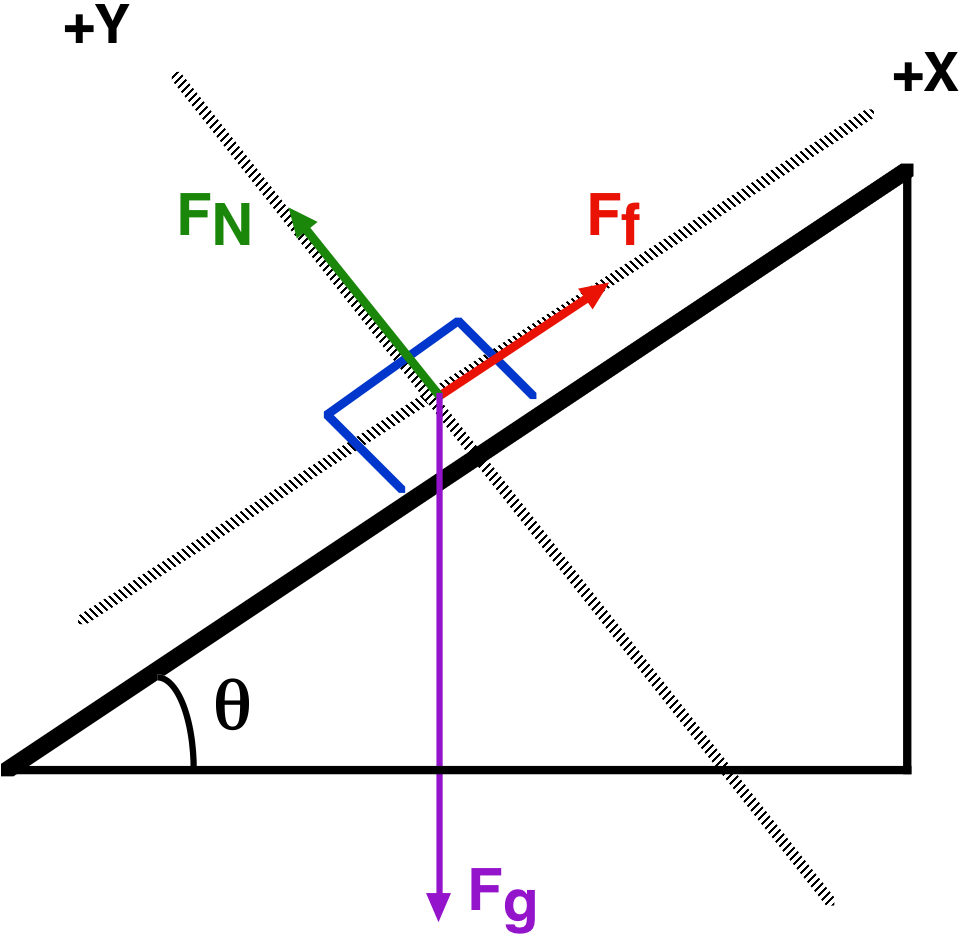
Finding FN, the normal force.
In this diagram, the purple vector represents the gravitational weight of the block. Notice that in this case, the weight is NOT perpendicular to the frictional surface. Therefore, the weight is not equal in magnitude to the normal force FN as was the case in horizontal frictional surfaces.

Instead, we resolve the weight x and y components. Fg y is constructed perpendicular to the frictional surface. Its magnitude can be calculated when the weight mg and angle are known.

However, due to the geometry of the diagram and the fact we need the angle from the positive x axis, which is tilted, we must subtract this angle from 90 degrees for the remainder of this problem.

The normal force FN is equal in magnitude to the y component of gravity:
Fgy = mg sin(90-θ)

Finding the Ff, the frictional force.
Once the weight vector has been calculated, the x component of the weight can be calculated with by:
Fgx = mg cos(90-θ)
This x component of gravity is parallel to the frictional surface, and represents that component of the weight, which points down the ramp, providing the applied force.

The Frictional force Ff is equal in magnitude to Fgx.

7.2 Projectile motion is a particular kind of 2 dimensional motion.

• Projectiles are objects which are launched from some sort of device such that after launch, there is no more unbalanced force in the horizontal dimension.
• The only force continuing to act on the object is gravity. Such objects may be said to behave ballistically. Examples of projectiles would be balls hurled by hand, bullets shot from guns, arrows, divers jumping off cliffs, etc.
• Projectiles define a parabolic pathway to the Earth.

For most of the problems we will deal with in this section, we make the following assumptions:  

• The only force present after launching is the force due to gravity. There is no acceleration in the horizontal, or "x" dimension. i.e., we disregard other forces such as air resistance.
• The acceleration due to gravity is g = -9.8 m/s ² .
• We choose a coordinate system in which the positive y-axis points up perpendicular to the earth's surface. This definition gives, a_y = g and a_x = 0 .
• The rotation of the earth does not affect the motion.

Independence of Motion in Two Dimensions

Imagine a bullet fired from a rifle barrel that is horizontal to the ground, as in the diagram below . Then imagine a second bullet that is dropped directly to the ground, from the same heigth as the rifle barrel, and at exactly the same time the first bullet is fired. Which bullet will reach the ground first? Answer... barring obstacles and air resistance, they will both reach the ground at the same time! Although the "fired" bullet is moving horizontally with more or less constant velocity, it is accelerating toward the ground under the same rules of gravity as the bullet that was just dropped, (-9.8 m/s/s).
 

• This downward acceleration is independent of the bullet's horizontal velocity.
• The horizontal velocity is independent of the acceleration.
• However, keep in mind that the time t_x the bullet will have to travel horizontally is the same as the amount of time t_y required for the bullet to reach the ground as it travels through the vertical dimension under the rules of gravity!

 Click your RELOAD button if you missed the animation. It only runs 6 times/loading!

• Now, calculate the length of time required for both bullets to reach the ground if they are fired/dropped from a heigth of 2.0 meters above the ground level:
  • Use y = V_yit + 1/2 gt² (V_yi = 0 in the vertical dimension), and solve for time.
• Remember that the amount of time the bullet can travel horizontally is limited by the time it takes to fall to the ground due to the acceleration of gravity, g.
• Use the time you calculated above to answer the question: How far (x) will the "fired" bullet travel horizontally in this amount of time if its horizontal velocity is 100 m/s?
  • Use x = V_x t

• 1. Separate the motion into the x (horizontal) part and y (vertical) part. The x component typically is some constant velocity v_x. The y component typically is some acceleration a_y
• 2. Consider each part separately using the appropriate equations. The equations of motion become as follows:
  • (a = acceleration, v = velocity, x = displacement in the horizontal dimension, y = displacement in the vertical dimension)
  • (a) x motion ( a_x =0): v_x = v_xi = constant

    • 1. x = v_xit

  • (b) y motion ( a_y = - g ):

    • 2. v_y = v_yi + gt 

      
      3. y = v_yit + 1/2at²

      4. v_y² = v_yi² - 2gy.
       

• 3. Solve the resulting system of equations for the unknown quantities.

Initial Conditions:

In projectile motion problems like the one above, it is handy to set up your problem solving structure as follows:
 

• We choose the coordinate system so that the bullet ( or ball, or particle, or whatever) leaves the origin ( x_i = 0, y_i = 0 ) at time t_i = 0 with an initial velocity of v_xi
• The horizontal distance ,x , is the range the bullet travels given v_x and the time the bullet requires to fall to the ground (which is the same amount of time it will have to travel horizontally!). v_x is the velocity in the x- direction; v_xi is the initial velocity in x-direction and v_xf is the final velocity in the x-direction.
• The vertical distance ,Y , is the height of the bullet above ground level. v_y is the velocity in the y- direction;v_yi is the initial velocity in y-direction and v_yf is the final velocity in the y-direction.

Use the same method outlined in Chapter 3 to solve problems in this section.

Calculate the time required for the ball to reach the ground, and the horizontal velocity:

BIG TIME HINT: Be sure that when you use any of the motion formulas listed here that all velocities and distances are in the same dimension within the formula. That is, don't use a horizontal distance in the same formula that includes a vertical acceleration!

Here's a .pdf that summarizes formulas, symbols and values used in parabolic motion

Here's a cool on-line page that does all kinds of trajectory calculations, it could help with your homework!

http://hyperphysics.phy-astr.gsu.edu/hbase/traj.html

2-D motion examples from class.