Physics Ch8.1

Ellipses

You need to come to class on the indicated day with an ellipse prepared on a piece of binder paper.

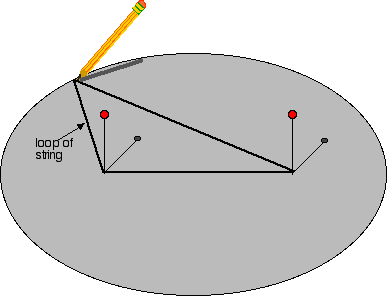
  • To make an ellipse, place your piece of binder paper over a piece of cardboard.
  • Stick two tacks about 10 cm. apart.
  • Tie a piece of string into a loop so that when placed over the tacks, you can stretch the loop with a pencil almost to the edge of your paper.
  • Move the pencil as shown around the paper to make your ellipse.
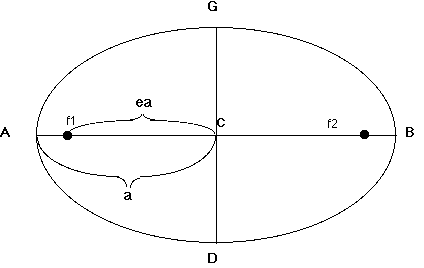
Study the diagram below. Line AB is the major axis of the ellipse.
  • Line DG is the minor axis of the ellipse. f1 and f2 are the two foci of the ellipse.
  • Lines CA and CB are the semimajor axes and lines CD and CG are the semiminor axes. Segment a is also a semimajor axis. Note that the foci are off center by distance ea.
  • The ratio of ea to the semimajor axis is the eccentricity of the ellipse, e.
  • The closer to the center the foci are, the smaller the value of e (the lower the eccentricity).
  • When the foci are at the center, ea is zero, and the eccentricity is zero, and the shape is a circle.
  • As the foci get farther from the center, the shape is more eccentric, and e is larger.
Now consider this ellipse to be representative of the orbit of a planet around our own Sun. (No planetary orbits in our system are as eccentric as this one.) Place the Sun at f1 and the planet at point B. At that point (apogee), the planet is farthest from the Sun than at any other point, and the gravitational force Fgof attraction between the Sun and the planet is weakest of any point on the orbit. As the planet moves to point A one half year later the planet is at its closest point (perigee), and Fg is at its greatest. Newton's Law of Universal Gravitation says that

1. . For any particular planet, Gm1m2 is constant, and that means that Fg is proportional to 1/d2, where d is the distance between the planet and the Sun. Another way of saying this is that Fg is inversely proportional to d2. If we assign an arbitrary value of 1.0 to the Fg at location A in the orbit, how does the Fg at location B compare to that?

Since Fg is inversely proportional to d2, that means that if d decreases, the force does the inverse, or increases. Further, if d decreases by a certain factor, Fg increases by the square of that factor.

Example..

  • In the case where the planet is at point B, the distance d between the planet and the Sun is f1-B. Let's make that value 12 AU.
  • Then move the planet to point A where d (A-f1) is only 2 AU.
  • By what factor has the distance d been reduced? 12/2 = 6.
  • d is 1/6 of the value it had when the planet was at B.
  • The force at A will be the inverse2 of this value, or (6/1)2 times the force at B. If Fg at B was 1.0, then Fg at A is 36.
  • Remember again, no planetary orbits in our system are really this eccentric, and therefore the difference in forces between apogee and perigee are not nearly as great as in this example.

return to chapter 8.1 notes