Kepler's Three Laws of Planetary Motion

Johannes Kepler (1571-1630), using data he stole from his one-time mentor Tycho Brahe, waged his own private "war on Mars" and discovered that the shape of Mars' orbit was not a perfect circle, but an ellipse. He then managed to deduce that the orbits of all the planets were also ellipses. It was fortunate that Kepler worked with Mars first, since its orbit was the most eccentric of the planets known at the time, and its secret was therefore the most discoverable! This concept became Kepler's First Law, the Law of Ellipses.

Further, Kepler determined that as a planet moves through its orbit, the area of the ellipse swept out by the radius of orbit in a given time period is equal to the area swept out by the radius of orbit at any point in the orbit during an equal amount of time. This became Kepler's Second Law, the Law of Equal Areas.

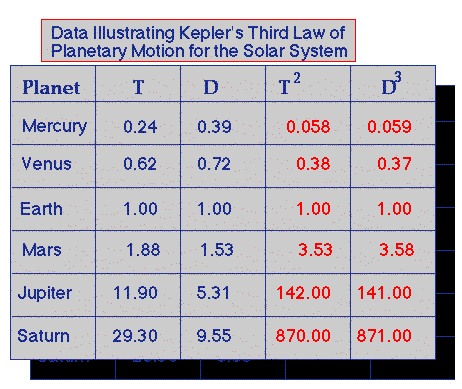
Finally Kepler determined that the ratio of the Period of Orbit (T) squared to the Radius of Orbit (r) cubed is a constant for any satellite of a central mass in an orbital system. For example,

1. using the period T of the Earth's orbit around the Sun (1 year) and the average radius of the Earth's orbit around the Sun (1.49 x 10¹¹ meters) produces the same value (3.0 x 10^-34 yr²/m³)as when the orbital information for Jupiter is used!

• The orbital information for Uranus also produces this number.
• It is a constant for our solar orbital system. So.

2. , and so on. So, for any system, = k, where k is a constant for that system.

This is Kepler's Third Law, the Law of Harmonies. We will see the derivation of the mathematical representation of this law shortly.

If you know the Period and radius of orbit for one planet, and the Period of orbit for another planet, you can easily find the radius of orbit for the second.

Similarly, when you use data for satellites of the Earth itself, a constant will also be obtained for any satellite of the Earth.

This will be a different constant from that obtained for the Sun.

• Square of any planet's orbital period (sidereal) is proportional to cube of its mean distance (semi-major axis) from Sun
• Example - If a is measured in astronomical units (AU = semi-major axis of Earth's orbit) and sidereal period in years (Earth's sidereal period), then the constant k in mathematical expression for Kepler's third law is equal to 1, and the mathematical relation becomes T² = R³ . This is a useful value to use when comparing orbital data of other planets to that of Earth. Look at thiis table:

• You try: The period of the Moon's orbit around the Earth is 2.36 x 10⁶ seconds. It's mean radius of orbit is 3.8 x 10⁸ m. Find the orbital constant for the Earth. You should arrive at 1.0 x 10^-13 sec²/m³.
• Find the period of orbit T_sfor a man-made satellite whose radius of orbit r_s is 7.19 x 10⁶ meters.Use the format :
  • 3. and solve forT_s or use the Earth-satellite constant you got above in place of
• You should arrive at about 6.1 x 10³ seconds.
  • This is the approximate orbital period of the polar-orbiting NOAA satellites that we monitor in the back of the room.
  • We take photos of Earth directly from these satellites, and it is this knowledge of its orbital characteristics that allows us to be able to predict when the satellite is overhead so we can have the radios and computers turned on at the right time!

Video: Kepler's Laws Of Motion, from the Mechanical Universe Series.

Activity: The Orbit, page 179. Come to class with an ellipse already drawn as shown in the activity and the video.

Homework: Set 1: Chapter 8 questions 1-8 set #2 problems 31-32, 34-39

Universal Gravitation

Newton realized that the force that caused apples to fall toward the earth also causes the moon to fall toward the earth.

• The apple falls straight down because it has no horizontal motion; the moon does not hit the earth as it's falling because of its horizontal motion.
• If the moon was not moving horizontally it would hit the earth.

The force the earth exerts on the apple and the force the earth exerts on the moon is given by the same equation, known as Newton's Law of Universal Gravitation.. The law is expressed mathematically as

5.

• where F_g is the Force of gravitational attraction between two masses m₁ and m₂,
• G is the Universal Gravitation Constant (6.67 x 10^-11 N-m²/kg²)
• and d is the distance between the centers of the two masses. Note that G is UNIVERSAL... that means it is the SAME value everywhere in the Universe.

Now, if we combine Newton's Law of Universal Gravitation with his Second Law of Motion as it applies to objects in centripetal motion, we come up with something quite interesting. Remember that planets around the Sun, for example, are displaying centripetal motion. That means that they are being centripetally accelerated according to

6. just like the rubber stopper in chapter 7.

But in this case, the planet is not connected by a string to the Sun. Soooo... what is supplying the necessary centripetal force that keeps the planets in their orbits?

GRAVITY...gravity according to Newton's Universal Law of Gravitation!

7. and the centripetal force on an object in circular motion was (from chapter 7) is

8. where m was the mass of the object moving in the circle , r is the radius of its orbit, and T is its period of orbit. This tells us that

9. .

Lets talk specifically about the Earth orbiting around the Sun here. On the left side, m is still the mass of the object in orbit, the Earth. There are two masses on the right side. Let m₁ be the mass of the Sun and m₂ be the mass of the Earth. Remember... the Universal Law of Gravitation is the gravitational force of attraction between 2 masses, and here this force is supplying the centripetal force keeping Earth in its orbit around the Sun. Also, r and d represent the same value, the radius of orbit of the Earth around the Sun.

Notice from equation 9. above that the mass of the Earth cancels out of the equation, leaving (and I'm replacing d with r here, since they represent the same value) this equation:

10. . (note that this gives us a new value for a_c, which we will use later.

With a little rearranging I get

11. .

• Remember.. the T and the r are properties of Earth's orbit, and m₁ is the mass of the sun. Newton knew that the value of G would be a constant, and therefore, for any mass m₁ at the center of an orbital system, the entire right side of the equation must be a constant.
• So then, determined Kepler in his Third Law, must the left side of this equation be constant for any satellite of the central mass!
• The actual value of G was not determined until about 100 years after Newton's discovery of the relationship. Henry Cavendish did this for us.
• If you use known orbital information for a satellite of any system with a known mass m₁ at its center, G always calculates out to be constant.
• Both sides of formula # 11 represent the "Keplerian constant" for an orbital system.
• VERY IMPORTANT: Note from formula #11 that if you can determine T and r for any satellite, you can determine the mass of the body at the center of the orbital system.

Now.. before we go any further.. back to the Law of Universal Gravitation (formula #5 above) for a second. The constant G does not depend at all upon what masses are being considered, where they are in relationship to one another, or what their state of motion is. Think about a person standing on the Earth's surface. Is there a force of gravitational attraction between the Earth and the person (masses m₁ and m₂, respectively)? Of course there is, and the Universal Law can be used to calculate that force.

You try: Calculate the force of attraction between the Earth and you!

• Use the mass of the Earth (5.979 x 10²⁴ kg) as m₁and your mass in kg (probably about 80 kg) as m₂.
• So, what do you use for r? Well.. r is the distance between the centers of the masses. You are standing on the edge of the Earth who's radius r_e(NOT THE RADIUS OF ORBIT) is 6.3713 x 10⁶ meters.

• You can add the extra 1 meter from the Earth's surface to your belly button if you want, but I really don't think its significant here. The accepted value for radius of the Earth is sufficient to represent the distance between the two masses.
• Using 80 kg as my mass.. I arrive at 7.8 x 10² Newtons for the gravitational force of attraction. between a person and the Earth. Remember when we used that VERY SAME PHRASE as the definition of weight?? Check this out:
• Before, we used Fg (wt) = mg to calculate weight, where g is the acceleration due to gravity close to the surface of the earth (-9.8m/s²) and m is the mass of an object on the surface.Do you think you might get the same value for Fg this way as you did above? Only one way to find out! DO IT! YOU GET THE SAME STINKING RESULT. Amazing, eh?

Henry Cavendish (1731-1810) knew about this result also. He knew that

12. = mg. m is the same as m₂ in the Universal Law equation, and m₂ cancels out of both sides leaving

13. .

The value of g (-9.8 m/s²)was already known at Cavendish's time, thanks to Gallileo, and Eratosthenes had discovered the radius of the Earth a long time before. Cavendish himself determined the value of G experimentally. The only unknown in the expression is m₁, the mass of the Earth, which Cavendish simply solved for.

You try: "Weigh the Earth" by solving formula 13 for m₁. Compare your answer to the value stated in your textbook.

Chapter 8 activities:

Videos: "Kepler's Laws

Activity: The Orbit.