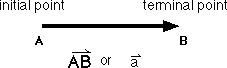
| ERHS PHYSICS
Chapter 4 Notes: Vectors |
||||
|
|
||||
Six easy steps to solving any vector addition problem can be found here.
Vectors are graphic representations of vector quantities. Vectors are also rreferred to as directed line segments which are straight lines with arrowheads on them which indicate direction. The length of a vector, or directed line segment, indicates the magnitude of the vector quantity it represents. The beginning of a vector, or directed line segment, is called the initial point, and the other end, with the arrowhead, is called the terminal point. Notice the two methods of labeling a vector:
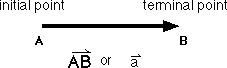
Two or more Vectors can be added two ways:
Method I: Place the tail of one vector at the head of the other vector.
The resultant vector is consctructed FROM the tail of the first vector in the series, TO the head of the last vector in the series. This RESULTANT is also a vector, and represents the sum (or NET) value of all of the others in the series. A resultant of a vector addition series can be used to replace/represent all of those other vectors!
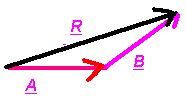
Draw vectors A and B to scale then simply measure the answer with a ruler.
To find the answer mathematically requires the use of the Laws of Sines: and Cosines:
Law of Cosines: If the angle between A and B above is theta, then 
Method II: Let all the vectors begin at the same point. Then break-down each vector into its horizontal components- then algebraically add each one. Next breakdown each vector into its vertical components- then algebraically add each
one. From these two components then find the resultant vector. This method is the most logical way of visualizing force vectors; and the math is easy.
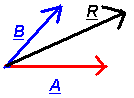
The main advantage in this method is that you avoid using the Laws of Sines and Cosines. If we can make a bunch of vectors that are all at right angles to each other, they become very simple to add, and will produce right triangles which are easy to solve.
Think of vectors as being the legs of a right triangle, then the resultant vector will
be the hypotenuse.
Note that the angle ø , is that angle between c and a.
Know the following relationships;
(1) sin ø = b/c , then solve for b: b = c sin ø .
(2) cos ø = a/c , then solve for a: a = c cos ø
a is now defined as the horizontal component of the vector c; b is defined as the vertical component of vector c; and c is the resultant vector. Or you can say that if you add vectors a and b the answer will be vector c.
What we are doing here is realizing that any vector (straight line) whose magnitude is known can be defined as the hypotenuse of a right triangle. Knowing the hypotenuse of a right triangle allows you to define the base and altitude of the triangle. These are known as the horizontal and vertical components of a vector (hypotenuse). So.. to add vectors one may resolve each vector into its horizontal and vertical components, and then add all these components. Since horizontal and vertical are perpendicular planes, components which lie in those planes are perpendicular to each other, and will produce right triangles when added head to tail. Again, right triangles are very easy to solve.
(3) Remember that vectors must have a direction. To get this direction find the angle whose arctangent is b/a.
tan ø = b/a so, ø = inverse tangent b/a. Make sure you know how to determine the angle in degrees when the tangent is known. Finding the arctangent is usually done on a calculator with the inverse-tangent function.
Method I:
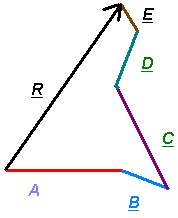Graphical addition of these are easy, just draw all vectors to scale then measure the resultant with a ruler.
Method II:
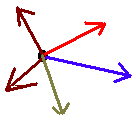using Method II, these become easy problems.
In a force problem, this is simply the force you must add in order to have zero acceleration, or that vector required to bring all other vectors in a system into equilibrium. Using the free body diagram method, this becomes easy to find. The equilibrant force is that force (or any other vector value) that causes equilibrium.
Extremely important: In a vector system that is in equilibrium, it is essential that you remember that the resultant of all vectors is ZERO. This also means that the resultant of all horizontal components of these vectors is zero, and the resultant of all their vertical components is also zero!
This is similar to what we did previously where we added two vectors to find the resultant. In this section we are given the resultant and we are trying to find the vertical and horizontal components (which will be perpendicular to each other). ANY single vector can be regarded as the resultant of two other perpendicular vectors, known as the perpendicular components. This makes solving vector problems that involve vectors acting at weird angles much easier. You get to turn everything into right triangles!
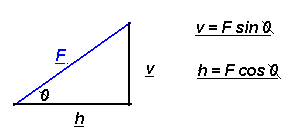
where F is the given vector and h and v are its perpendicular components; and ø is the angle between h and v.
To find the horizontal component of the vector F, first find the cosine of the angle and then solve for h.
cos ø = h/F , then h = F cos ø .
To find the vertical component of the vector F, first find the sine of the angle and then solve for v.
sin ø = v/F , then v = F sin ø
These represent an important class of problems involving sliding boxes up and down an inclined plane where you have friction. In the following instance, imagine a block of wood set on a wooden ramp. The ramp is slowly raised from horizontal while someone taps the ramp with a finger to cause a vibration which prevents static friction. The ramp is raised to the point where the block just begins to slide. At this point, the frictional force, Ff which points up the ramp has just been equaled by the applied force, supplied by the component of gravity pointing down the ramp!
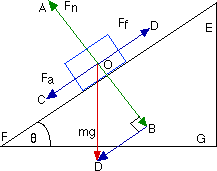
Finding Fn, the normal force.
In this diagram, vector OD irepresents the gravitational weight of the block. Notice that in this case, the weight is NOT normal to the frictional surface. Therefore, the weight is not equal in magnitude to the normal force Fn (vector OA) as was the case in horizontal frictional surfaces.
Instead, we resolve the weight vector OD into its components OB and OC. OB is constructed normal to the frictional surface. Its magnitude can be calculated when the weight mg and angle BOD are known.
Triangles DOB and EFG are similar triangles, and angle theta is similar to angle BOD.
The normal force Fn (OA) is equal in magnitude to OB.
Finding the Ff, the frictional force.
When the weight vector OD is resolved, the component BD can be calculated with the knowledge that angle BOD is similar to angle theta. Vector component BD is parallel to the frictional surface, and represents that component of the weight which points down the ramp, providing the applied force Fa.
Force Fa = vector BD, and the Frictional force Ff is equal in magnitude to Fa.
Special note: Examine the right triangle DOB. Notice that the side opposite angle BOD is equal in magnitude to the Frictional force Ff, and that the side adjacent to that angle is equal in magnitude to the Normal force Fn. Since Ff/Fn = coeff. of friction, and the opposite/adjacent sides = the tangent of an angle, the tangent of angle BOD is equivalent to the coefficient of friction! Remember earlier that we said that angle theta is similar to angle BOD? Hmmmmmm...... Lab time!
Note: weight = ma, where a = g (-9.8 m/s-s near the surface of the earth). Remember that the unit for mass is the kilogram and the unit for force (weight) is the Newton.
set#2. page 78-79, questions 7-10, problems 21-24
set#3. page 79 problems 27-31
online practice: This website has a tutorial, and a way to type in various vectors and get the resultant
Here's another online vector practice site:http://www.explorelearning.com/index.cfm?method=cResource.dspResourcesForCourse&CourseID=330
video: "Vectors"
Lab#1 : Textbook, page 69: "The Paper River"
Lab #2: finding the coefficient of friction of a block on an inclined plane.