
| ERHS PHYSICS
Chapter 9.2 Notes |
||||
|
|
||||
video: "Conservation of Momentum" from the Mechanical Universe Series. 19 min.
We study collisions between two objects in this section. The two objects (or particles) may both be moving, or one may be at rest. Also, the two particles may be moving in opposite directions, or both moving in the same direction! The objects may bounce off of each other, or they may stick together. They may move off in opposite directions after the collision, or they may move off in the same direction.
In the case of two colliding objects, such as the locomotives shown here..

Locomotive "A" has a momentum ![]() and loco "B" has a momentum of
and loco "B" has a momentum of ![]() .
.
The expression that shows what happens to the A train's momentum is ![]() and
and
the expression that shows what happens to the B train's momentum is ![]()
The law of conservation of momentum says that ![]()
You Try: The mass of train A is 2.5 x 104 kg and is moving at +10 m/s. The mass of train B is 1.0 x 104 kg and is moving at -12 m/s. There is a collision, and the two trains stick together. Note: when two objects stick together like this, their masses combine into one, and there is only ONE velocity.. that of the combined mass.
a. What is the momentum of this system BEFORE the collision?
b. What is the momentum (p') of the system AFTER the collision (two trains stuck together)?
c. What is the velocity vab of the two "stuck-together" trains after the collision?

You Try: Assume that we have the same two locomotives (same mass, same velocity) as indicated above. Again they collide, but this time they do not stick together. Instead, the larger train A continues on with a velocity of + 2.0 m/s. What is the velocity of the smaller train after the collision?
Try some more: Do the practice problems #7-12 on page 210
System – A collection of particles or object chosen for observation and analysis
Closed system – A system that doesn’t gain or lose mass
Isolated system – A system with no external forces
Internal forces within a system cannot change its momentum, but external forces can change the momentum of a system. Many of the problems in this section will involve explosions within a system; remember that the total momentum before the explosion will equal the total momentum after the explosion.
Another way of looking at the law of conservation of momentum is that after any interaction between particles in a closed, isolated system, the system momentum remains unchanged even though the respective velocities of the particles has changed. That is, the change in the system's momentum is zero. Momentum is conserved. In most cases, the masses of the particles does not change during such interactions, so any change in momentum of a particular particle is due to the velocity change after the event, and change of momentum in one particle is equal in magnitude but opposite in direction to that of the other. In the case where there are only two particles involved in such an interaction, this relationship is expressed as
![]()
You try: work through the example problem on page 188, and then work practice problems 7-12 on page 210.
The Law of Conservation of Momentum also holds for motion in two and three dimensions. Look at the diagram on page 190 in your text.There are two billiard balls here, one moving and one not moving. The net momentum of this system is just the momentum of ball "A", since the other's velocity is zero. Note particularly the vector which represents the momentum of the system before the collision. According to "LAW"... the system's momentum vector AFTER the collision must be identical. This system vector will be the vector resultant of the individual vectors of each ball after the collision! Given the interior angles in this problem, and side "c", you can solve for sides a and b. These values will be the respective momenta of each ball after the collision. Knowing the mass of each ball, and its momentum, it's easy to solve for velocity!
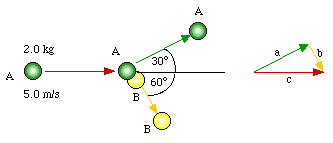
Notice how the vector diagram sets up.
Note that the MAGNITUDES of sides a and b do not add up to 10.0 kg m/s ! This is due to the vector nature of this problem, and indicates why you can't simply add the momenta of the two balls as you did when the involved objects all moved within the same dimension!
You try: solve practice problems 17 and 18 on page 216.
Homework: set #3 Ch 9 questions 5-10 p 217-218 set #4 problems34-42 p. 218-219