9:1 Impulse and Change in Momentum.

Here are some key concepts to remember:

• The physical characteristic known as momentum (p) is represented by the product of its mass
• and velocity:
  • 1. p = m * v
• The units for momentum are kg * m/s. (N * s, the units for impulse, can be used interchangeably).
• Momentum is a vector quantity. Its direction is always the same as the velocity. The change in momentum will be in the same direction as the impulse which produced it.
• Impulse is a vector quantity acting in the same direction as the force which caused the impulse.
• The units for impulse are N * s.
• Impulse and momentum may be regarded as "cause and effect". An impulse produces a change in momentum.
• The area under a force versus time graph can be used to determine the impulse (provided that the direction of the force producing the impulse is not changing).
• The impulse of a force is the product of the force and the time throughout which it is applied
  • 2. I = F * t
• A system is a defined collection of particles, and an isolated system has no external forces acting on any of its particles.

Here we go:

In this chapter we study the results of systems of particles instead of individual particles.

Momentum is defined as mass times the velocity of an object, and is derived from Newton's Second Law.

3.

therefore

4.

The left side of this equation represents impulse. F is the average force applied throughout a time t

The right side of the equation is known as momentum.

In general, momentum is written as. As long as no unbalanced force is applied, the momentum of a constant will remain constant.

This expression represents linear momentum, when objects are moving in a straight line. Objects in circular motion will experience a change in momentum too, if a torque is applied. The result of this is called angular momentum.

If the mass of the object remains constant, and an unbalanced force IS applied, then the resulting change in momentum is

5.

Note that this statement indicates that changing the velocity produces a change in the physical property known as momentum. Remember that in order to produce a change in velocity, an unbalanced force is necessary.You cannot apply a force with no change in time, therefore an acceleration is implied as well, and the applied force, acceleration and change in velocity are all in the same direction.

You try: Find the momentum of of a 1000.0 kg vehicle traveling at 88.0 km/hr.

you need to convert the km/hr into m/s. (S.I. only!.. kg,m & s)

now, so

Try this one:

If your velocity changes, then your momentum changes, right? Right. Suppose you step off a chair that is 0.50 meters high, and your mass is 75 kg. At the instant you reach the ground, you will have achieved a final vertical velocity according to

8.

and a moment later your velocity will change to zero. Assume the initial vertical velocity is zero. Find your change in velocity and resulting change in momentum!

Ok.. your final velocity = 3.13 m/s downward.

your change in velocity when you stop is = 0.0 m/s - (-3.13 m/s) = 3.13 m/s and

your change in momentum = 75 kg x 3.13 m/s = 2.3 x 10²

The concept of applying a force throughout a specific time increment now has a name: Impulse.

You try: What impulse results from the application of a constant force of 15.0 Newtons over a time period of 6.0 seconds?

Impulse = Ft = 15.0 N X 6.0 sec. = 90 .

A given net force applied to a specific mass can only produce one value acceleration according to Newton's second law:

F = ma.

And if we specify a time duration, this acceleration can only result in one value for change in velocity since

6.

Therefore, a specific impulse produces a specific change in momentum.

We then define (7.) as the impulse-momentum theorem.

Note that while these two values will have the same mathematical magnitudes, they represent two different concepts. Impulse IS NOT THE SAME as momentum. However, since one is the direct result of the other, and since any given impulse can only produce one value of momentum change, each value can be calculated in terms of the other. The magnitude of a change in momentum will be the same as the magnitude of the impulse that produced it.

You try: What impulse was given that produced a +10.0 m/s change in velocity to a mass of 3.0 kg?

• The change in momentum = 10.0 m/s X 3.0 kg = 30
• so: the impulse required to produce this momentum change has the same magnitude:
• Impulse =30 .

You try: Recall the jumping- off -the-chair problem from earlier. Suppose you kept your knees locked and the time required to produce the change in momentum (the time to change your velocity from -3.13 m/s to zero) is 0.09 seconds. What is the force of the impulse?

• The magnitude of the impulse is the magnitude of the momentum change as in expression (7.) above. So
• Ft = 2.3 x 10² . These units are the same as
• so the impulse here is Ft = 2.3 x 10² . From expression (7.) above
• (9.) so
• = 2.6 x 10³ Newtons! That's equivalent to over 500 pounds.

  Remember that since you changed your momentum here by a specific amount, there is ONLY one impulse that could have produced that. There are, however, an infinite combination of forces and times are possible that can produce this impulse. If a person was interested in reducing the force applied to the knees in this kind of activity.. the only way to do so is to lengthen the time over which the force is applied. This can be done by simply bending your knees as you land. The more time you can take to bring your body to a complete stop, the lower the average force delivered to your poor old knees! Imagine how you could accomplish taking the MAXIMUM time possible to stop as you stepped off the chair.

All this information works very well so far, as long as the impulse force is constant throughout the given time period. But what if the force is NOT constant? In reality, this is more often the case. What you do then is to simply graph the force as a function of time like this:

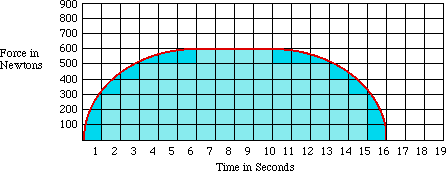
Impulse can be determined by finding the area under the Force-Time curve! Count up the squares here, or use a little of your calculus background( except you don't know the function that produced this curve). The area under this curve is 7.8 x 10¹ .How much change in momentum was produced? If the mass that the force was applied upon was 100 kg, how much velocity change was there?

Do practice problems 1-6 on pages 204-205.

bunning '98