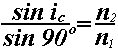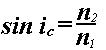Chapter 17.2 Notes

An incident ray striking a boundary from a more refractive medium to a less refractive medium at an angle greater than the critical angle experiences total internal reflection.(Arizona State module)

Total internal reflection is only possible if light is travelling from a more refractive medium to a less refractive medium. ( i.e., n_r < n_i )

As the angle of incidence increases, the angle of refraction approaches 90 degrees. See Diagram

The critical angle is the angle of incidence for which the angle of refraction is 90^o. At this angle the refracted ray passes parallel to the boundary. See Diagram.

The incident ray undergoes total internal reflection at any angle greater than the critical angle. See Diagram.

If the incident angle is less than or equal to the critical angle, the refracted ray will be bent away from the normal (provided that n_r < n_i ) .

A high relative index of refraction (the ratio n_r/n_i) will result in a smaller critical angle.

The critical angle (i_c) can be determined from the general form of Snell's Law. At the critical angle, the angle of refraction = 90^o, so sin r = 1, and

since sin 90 ^o = 1 ,

Newton's experiments illustrated the dispersion of sunlight into a spectrum (and recombination into white light). Sunlight consists of a mixture of light with different wavelengths. A dispersive medium is one in which different wavelengths of light have slightly different indices of refraction. For example, crown glass is a dispersive medium since the index of refraction for violet light in crown glass is higher than for red light. This is responsible for chromatic aberration. (Manufacturers of optical glass customarily specify the refractive index of a material for yellow sodium light, the D line.)

You can see a very cool internet site version of the prism above, where you get to control a laser beam through a prism. You get to change the wavelength, and see what happens to the refraction angle. Notice that there are a couple of "x's" on the page.. move them to the edge of the prism and center them on the point of intersections, then click the "tools" popup window. You can measure angles of refraction! Caveat.. this site requires the "shockwave" plugin for your browser.

Light passing through a rectangular prism can experience lateral displacement. In a prism with non-parallel sides, the displacement is described by the angle of deviation between the ray incident to the prism and the ray emerging from it.

Many examples found in commonly observed phenomena and practical applications illustrate refraction and total internal reflection. (Several should be described and discussed or researched independently by students.)

Glossary of Terms

Homework: Set #3: questions 10-14

Set #4 Ch 17 problems 50-57

Activities:

Do this 'paper' refraction/internal reflection activity.

1. Use a laser beam to experimentally determine the critical angle for a rectangular lucite lens, and then determine the index of refraction for the material.

2. Use the laser beam to observe total internal reflection in a test tube containing a suspension of borax particles, and in various light pipes such as lucite, small optical fibers, and a curving stream of water.

3. Use a ray box to produce a beam of white light, and observe dispersion as the beam is passed through a prism.

Links: Here is a location with some fun on-line activities with light. Check out the pages on optics. Your browser needs the Macromedia Shockwave Plug-in installed first.