Definition:
Wave – an oscillating disturbance that travels through a medium from one location to another location

Properties of Waves:
Amplitude (A) – maximum amount of displacement from the rest position
Units: m

Wavelength (l) - the length of one complete wave cycle
Units: m (nm is used for light!)

Frequency (f) – the number of complete vibrational cycles of a medium per a given amount of time
f=1/T
Units: Hz = 1/s

Period (T) – the time it takes to make one vibrational cycle (one wavelength)
T=1/f
Units: s

Speed (v) = the distance traveled by a given point on the wave in a given interval of time
v=l*f =l/T
Units: m/s

Transverse vs. Longitudinal Waves
Transverse: a wave in which the particles of the medium are displaced in a direction perpendicular to the direction of energy transport
Longitudinal: a wave in which the particles of the medium are displaced in a direction parallel to the direction of energy

Section 1: Types of Waves

Waves can be thought of as travelling energy. Waves are produced by some kind of oscillator. If there is only one cycle of vibration from the oscillator, a single pulse of energy will be produced that radiates away from the oscillator. If the oscillator repeats the vibration, a wave train will be produced.

There are two principle types of waves for us to examine at this point: Mechanical and Electromagnetic.

Mechanical:

• require a medium of some kind in which to travel. The energy displaces the medium in some way as it passes through.
• Depending upon how a wave displaces the medium with respect to the direction of travel of the energy, mechanical waves can be classified as either
  • a. Transverse waves where the medium is displaced perpendicular to the direction of travel of the energy. Waves on a vibrating guitar string are transverse waves.
  • b. Longitudinal waves where the medium is displaced parallel to the directino of travel of the energy. Sound waves that produce alternating areas of compressed and rarefied air are longitudinal.
  • c. Surface waves, which are a combination of transverse and longitudinal. Seismic waves are surface waves.
• Examples: Sound waves, waves on water, seismic waves

Electromagnetic:

• do not require a medium, can propagate across a vacuum
• example: radio, tv, microwaves, light waves
• electromagnetic waves will be discussed in more detail in subsequent chapters.

Wave characteristics:

If waves are produced by an oscillator that repeats it's cycle regularly, then a series of pulses called a wave train results.

• The number of such pulses produced per second is called the frequency of the wave.
• Frequency is always expressed in terms of the number of waves (or oscillations or cycles) per second, and the commonly accepted unit is the Hertz (Hz). Frequency in wave formulas is indicated by the letter f.
• One Hertz is one wave per second.
• In sound waves, humans perceive frequency as pitch.

The speed at which a mechanical wave passes through a given medium is generally fixed for any given set of conditions.

• For example, the speed of sound through air is about 343 m/s , but this depends upon the temperature, pressure, humidity, etc at the particular moment. A good approximation of speed of sound through water is 1500 m/s
• Since an energy wave does have a definite speed of travel, as soon as it emanates from the oscillator, it begins to move away at this velocity.
• The first pulse produced will have moved a calculatable distance away in a specific amount of time, say one second, before the next pulse is produced and starts to follow the first one!

Check it out:

• Lets say an oscillator, like a finger poking into a pool of water, vibrates at a rate of 2 times per second (2 Hz) and produces surface waves that travel at 0.5 meters per second.
• At the frequency of 2 Hz, a new wave is produced every half-second, right? Right! This value is called the period of a wave.. the amount of time required to produce one wave, or the amount of time between two successive waves travelling at the same velocity.
• Period is designated with a T in wave formulas. Note that the period of 1/2 second/wave is the INVERSE of the frequency.. 2 waves/second! Keep this in mind.

  Ok.. if the first wave is produced and radiates away from the finger at 0.5 m/s, how far away will it be before the next pulse is produced? Well.. the second pulse will be produced 1/2 second after the first (TWO waves per second, remember?) and at 0.5 m/s the first pulse has travelled a distance of 0.25 m. ( d = v x t ). So.. the second pulse has it's crest 0.25 meters behind the first. This is the wavelength of the wave, or lamda ()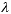

So.. to arrive at wavelength, we multiplied speed times period: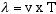

But period and frequency are inverses of each other, so we could just as well write this formula as

If you solve this equation for velocity, you arrive at the basic wave formula:

The amount, or distance from some resting point, that a wave displaces the medium it is travelling through is called the amplitude of the wave.

• In sound waves, increased amplitude is perceived by humans as increased loudness.
• In light waves, increased amplitude is perceived as increased intensity or brightness.
• Amplitude of a wave is independent of its speed, wavelength or frequency.

This diagram illustrates the features of a sine wave, but the same features can be identified on any type of mechanical wave.

Demonstrations: Mechanical waves on a long spring.