ERHS PHYSICS Chapter 10 Notes

10:1 Work and Energy

The physical definition of work is different that the everyday definition.

• In physics, work is the product of an unbalanced force applied through a distance, and is calculated as the product of Force times distance:
• W = Fd (don't confuse this "W" with Weight!)
• The distance used must be through the same dimension as the applied force.
• The unit of work is the Newton-meter (Nm) or Joule.
• Every time you do work on a particle, or system of particles, the energy of that particle or system is changed. All such processes tend to contribute to the relative DISORDER of the universe! (Doing work increases the entropy of the universe, a subject we will look at later)

In order to move something, you have to apply a non-zero net force over a given time period.

• This is impulse, as you recall.
• This produces a change in velocity and therefore a change in momentum of the object.
• Since any change in velocity involves distance, then changing the momentum of an object requires that work be done on it!

Notice that the Work formula is not dependent upon TIME. For example..

• If two students are assigned to push identical cars across the parking lot at constant velocity, the amount of force required to overcome all the frictional forces should be the same.
• But, if one finishes before the other, the amount of work done is the same if the distances were also the same.
• There is something different here that relates to TIME, but it is not WORK!
• We'll discuss this concept later.

If you move something at constant velocity through the vertical dimension, then the force required is the weight (mg) of the object, and

W = mgd

You try: Study the example and do practice problems 1 and 2 on page 199.

• 1a. this is a simple application of the formula W = Fd. Just plug in the values
• 1b. Study the mathematical relationship between work and force. They are directly related. This means that if you double the force, the amount of work done is doubled, provided distance remains the same.
• 2a. Notice that the weight (mg) of the package is given. Assume here that we are asking only for the work done on the box by raising it vertically. Going up some stairs may also do some work in the horizontal dimension, but we have no horizontal force given in the problem.

If an object does not move, there is no distance involved, and work is not done on that object.

• If you push on a wall.. and the wall doesn't move, is there any work done? We have to be careful how we ask and answer this type of question. There is definitely energy being expended by your body, and no doubt some physiological work is done when muscle fibers contract, BUT.. the wall doesn't move and therefore no work was done ON THE WALL. No energy is transferred to the wall, and it doesn't gain any ability to do work itself.

When you make something move by doing work on it, that object gains energy.

• We can think of work as a mechanical means of adding energy to a particle or system of particles. In fact, the amount of work done is equivalent to the energy added! Consider a cart at rest: it has no kinetic energy and is not going to exert a force on any nearby carts. BUT.. do a little work on it by giving it a push, and the cart now has kinetic energy. Where did it come from? From the work you did on it. Further, it can now run into another cart, give it an impulse, and do work on it!

The unit for work is the joule, so one joule equals one newton times one meter.

Homework: Set #1: Chapter 10 questions 1-5, problems 19-22 page 241

Work and Direction of Work

What happens if you apply a force on an object, but the object doesn't move in the direction you applied the force! Consider the diagram of Mr. Rodriguez's one horsepower pickup truck below:

If the truck moves horizontally a distance of 10 meters, then work is done on the car. But the work is in a different dimension than the applied force. So, how do we calculated the work done? Well, the secret here is that there is a force that is applied in the same dimension as the distance traveled: it is simply the horizontal component of the applied force, and you know how to find that: VECTORS!

You try: First find the horizontal component F_x of the 5000 Newton force applied by the horse:

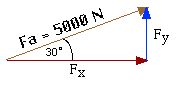
F_x = 5000 cos 30 and you should arrive at 4.3 x 10⁴ Joules of work done by the horse on the truck!

The effect of doing work on an object or system, no matter how it happened, is to give that object or system energy. If you made the object move, you gave it kinetic energy.

Power:

The rate of doing work is called power. Remember the two people we mentioned earlier, when one finished the same amount of work FASTER? This is an example of two different levels of POWER.

or

The unit of Power is the watt . One watt of power is equivalent to one Joule of work done every second, or one Joule/second.

Study the example problem on page 228-229 and work the practice problems 6-8 on page 229.

_________________

overheard in a local hardware store:

Customer: Do you have 2 4-watt bulbs?

Proprietor: Two what?

Customer: No, 4!

Proprietor: 4 WHAT?

Customer: Yes

Proprieter: No...

The Kilowatt-hour.

This is our most common unit of electrical energy around the household. Note that the kilowatt-hour (KWH) is a unit derived from Kilowatts X hours, or power X time.

Since power = work/time and work is the equivalent of energy, then energy = power X time. So the KWH is energy, not power even though we often talk about paying the "power bill". We purchase energy from the local gas/energy company in units called KWH. You probably pay around $0.12-$0.15 per KWH for household energy.

Question: if you operate a 100-watt light bulb continuously for 3 hours, how much energy is used in KWH, and how much would it cost?

answer: energy = power times time.

100 watts = 0.10 kilowatt (kw)

0.10 kw X 3 hours = 0.30 KWH.

At $0.15/KWH, the above amount of energy would cost $0.045 (4.5 cents)

How much energy in KWH would be used by the same light bulb if it burned for only 30 minutes?

100 watts = 0.10 kw

30 minutes = 0.5 hours

Multiply power by time: 0.10 kw X 0.5 hours = 0.05 KWH.

How does a KWH relate to a joule?

A joule is a watt-second.

There are 1000 watts per KWH so a KWH is the same as 1000 watthours. There are 3600 seconds in one hour, so 1000 watt-hours is the same as 1000 X 3600 wattt-seconds or 3.6 x 10⁶ watt-seconds, or 3.6 x 10⁶ joules. A lot!

1.0 KWH = 3.6 x 10⁶ joule

Lab Activity: "Your Power".. page 232. Addition: find out how a Horsepower compares to a watt, and find your power in Horsepower as well!

Homework: Set #2, Ch 10 problems27,29,30,31,32,34,36,37,41