| ERHS PHYSICS
Chapter 21 notes |
|||
 The Electric Field The Electric Field 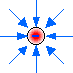
Recall that Coulomb’s law is very similar to Newton’s Law of Universal Gravitation.
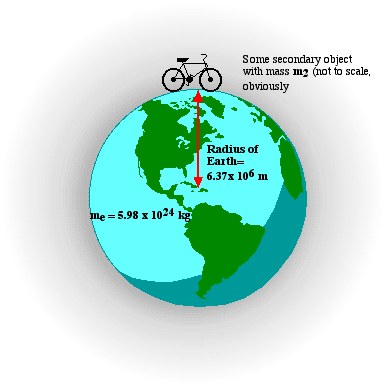
We used the symbol g to represent the strength of this field in Newton's Second Law formula: F = mg (F = ma!) We also learned that g near the surface of the earth was considered constant at -9.8 m/s2. Where does this value come from?
Check out Newton's Universal Law of Gravitation:
We can refer to the earth as the central mass in this system.
Near the surface of the earth, d is just the radius of the earth (6.37 x 106 m). In the Universal Gravitation Law, the values G, m1 and d are constant at the earth's surface, so we can give them a constant value. Solve the equation below for g, and see what you get:
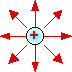
Surprise! (did you get 9.8 m/s2 ?) This value is the gravitational field strength of the earth, at it's surface and has units of N/kg which is the same as m/s2. N/kg can be read as Force per unit mass. What happens to g if d increases, as in the case where that secondary object gets significantly farther from the surface? g would decrease. That is to say that the strength of the gravitational field weakens. Similarly, another 'invisible force field' exists around a central charged object. You already know that a second charged particle near any other charge will experience an electric force. This force may be directed away from, or toward this central charged object depending on the signs of the charges. But even if there is NO second charged object, an electric field exists around the central object. A force will become evident as soon as a second charge is brought into the field. The electric field consists of an infinite number of points around a centrally charged object at which a second charge may exist. In the diagram, the electric field looks circular, but consider it to be more spherical, with no outer boundaries.
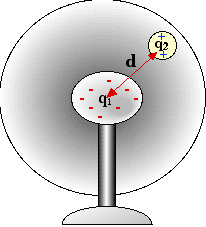
The electric field around a charged object has a strength that can be calculated and measured. At any particular distance from the object, the strength of the field depends upon the magnitude of the charge upon the object. There is no force until a second charge is brought to that location, but the field strength can be described in terms of force per unit charge, or Newtons of force per Coulomb (N/C) of charge on that second object, if it were there!
(incidentally... the two diagrams above are exactly the same size) If you examine the quantity Kq1/d2 from Coulomb’s law, you will find that by cancelling units, one is left with N/C, the unit we use to describe electric field strength. Furthermore, for any particular central charged object, E is constant. Electric field strength 'E ' can be calculated then, by the equation E = kq1/d2 where q1 is the charge on the central charged object creating the field and d is the distance in the field from that object. The field strength for any object depends upon d. Compare this to g in Newton's Law of Universal Gravitation Constant. Since we now know that E = kq1/d2 , substituting E into Coulomb’s law, we find that Fe = Eq2 and E = Fe/q2
Helpful link: http://physics.bu.edu/~duffy/java/EFielda7.html video: 'Electric Forces and Electric Fields ' from the Mechanical Universe Series. (15 min.) |
|||